物理音響モデルに基づく音響システムの研究動向
臨場感の高い音響を実現するために,さまざまな音響システムが研究開発されている。これらは,基本となる2チャンネルステレオのチャンネル数を増やすことでより高い臨場感の実現を目指すマルチチャンネル音響システムと,物理音響的な理論に基づいて音場の波面の正確な再現を目指す音場再現システムに大別することができる。本稿は,聴取エリア全体の音場の再現を目指す波面合成方式WFS(Wave Field Synthesis)や最適聴取位置における音の方向の再現を目指すアンビソニックス(Ambisonics)など,後者に関する理論的な背景と最近の研究例を紹介する。また,物理音響的なアプローチによって,異なるチャンネル数を持つマルチチャンネル音響信号間の変換を行う方式について解説する。
1. はじめに
音の臨場感を実現するうえで,音場再生・再現技術はきわめて重要な位置を占める。特に,近年は音の前後左右感だけでなく,音の上下感も表現できる3次元音響方式が提案され,その有効性が示されている。これらの方式には,2チャンネルステレオを拡張した22.2マルチチャンネル音響も含まれるが,本稿では,それ以外の物理音響的な理論に基づいて音場の波面の正確な再現を目指す方式について解説する。
音場の波面を聴取エリア全体で再現する方式の代表例はヨーロッパを中心として研究されてきた波面合成方式WFS(Wave Field Synthesis)である。日本でも,このような音場再現型の方式が研究されている。また,近年では最適聴取位置における音の方向の再現を目指す収音-再生方式であるアンビソニックスの研究が盛んになってきている。本稿では,音場再現方式として,2章で再生音場の周囲全体に設置したスピーカーで音場の波面を再現する方式について述べ,3章でWFSなど音場の片側にスピーカーを設置して音場の波面を再現する方式を説明する。4章ではアンビソニックスなど音の方向の再現を目指す方式について述べる。また,5章では,音の方向を再現する考え方をマルチチャンネル音響に適用して,チャンネル数の変換を行う方法について概説する。
2. キルヒホッフ-ヘルムホルツ(Kirchhoff-Helmholtz)の積分定理に基づく音場再現
波の伝搬や回折を説明する原理として,ホイヘンス-フレネル(Huygens-Fresnel)の原理が知られている。この原理は1図に示すように,伝搬する波の波面から2次波面が生成され,2次波面の包絡によって次の波面が生成されるという原理である。この原理をより厳密に記述したものが,キルヒホッフ-ヘルムホルツの積分定理である1)。
いま,音波が到来している場(音場)を音圧p(r, t)で表す。ここに,rは音場内の位置,tは時刻である。また,音圧p(r, t)のフーリエ変換*1 をp(r, ω)で表す。以下,フーリエ変換した後の周波数領域を用いて音場を記述する。音場内に2図のような領域Vを考える。2図においてSはVを囲む閉曲面,rAはV内の任意の点,nはS上の点rにおける外向き法線方向の単位ベクトルである。このとき,キルヒホッフ-ヘルムホルツの積分定理は,

で表される。ここに,jは虚数単位,kは波長定数,∂/∂nは法線方向(n方向)の偏微分を表す。(1)式において,関数

はモノポール関数と呼ばれ,音源の大きさが波長と比較して十分に小さい場合に全指向性音源からの音波をよく近似する関数である。(2)式は点rAに置かれた全指向性音源を表している。また,

はダイポール関数と呼ばれ,音源の大きさが波長と比較して十分に小さい場合に両指向性音源からの音波をよく近似する関数である。(3)式は点rAに置かれた主軸がn方向を向いた両指向性音源を表している。
(1)式の被積分項は境界上の点rに置かれた音圧勾配∂p(r, ω)/∂nに等しい強さを持つ全指向性音源と,音圧-p(r, ω)に等しい強さを持つ両指向性音源による点,rAにおける音圧の和を表している。従って,点,rAにおける音圧は境界面S上のすべての点rで積分したときの総和で表される2)。
キルヒホッフ-ヘルムホルツの積分定理はコンサートホールなどの原空間に設定された受音領域境界での音圧と音圧勾配を観測し,それを別空間の境界領域で再現することで原音場をそのまま再現できることを保証している。このアイディアは1960年代にCamrasによって提案された3)。この方法は原空間の受音領域境界に全指向性マイクロホンと両指向性マイクロホンを設置して音圧と音圧勾配を記録し*2,その値に基づいて再生空間の境界に設置されたモノポール音源とダイポール音源を駆動して元の音場を再現するというものである。3図にCamrasの方法を示す。Camrasの方法では,再生空間に無数の音源を設置する必要があるほか,音の全周波数帯域にわたってモノポール特性やダイポール特性を持つスピーカーが無いことが問題とされた。
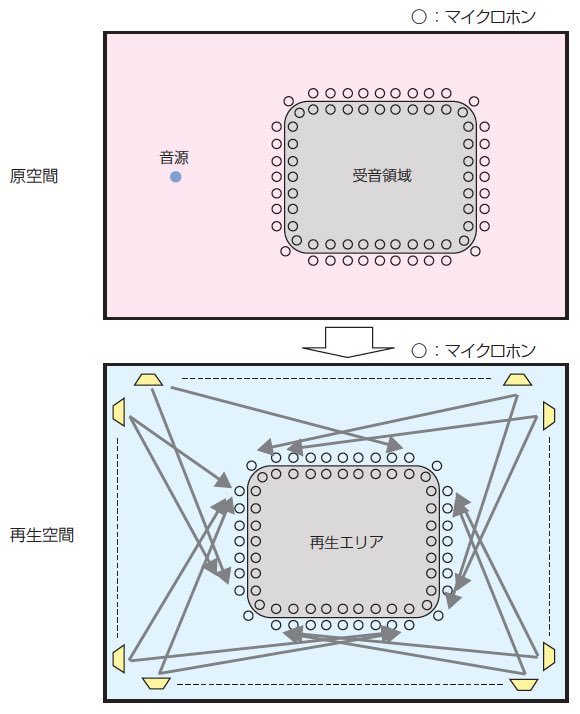
この問題を解決するために提案されたのが伊勢らによる境界音場制御法である4)。境界音場制御法の原理を4図に示す。4図において,境界面上に並んだ○印はマイクロホンである。境界音場制御法の特徴は再生空間を囲む境界領域にスピーカーを設置する代わりにマイクロホンを設置し,このマイクロホンで観測される信号が,原空間の受音境界領域で観測したマイクロホン信号と同じ信号になるように再生空間の周囲に設置したスピーカーの入力信号を制御するというものである。従って,境界音場制御法では,再生空間におけるスピーカーからマイクロホンまでの,いわゆる,多入力多出力(MIMO:Multiple Input Multiple Output)伝達特性の逆特性を解く必要がある。この逆特性を解くという問題は決して易しい問題ではないが,一度,再生空間において解けば,どのような原空間に対しても適用が可能である。



3. レイリー(Rayleigh)積分に基づく音場再現
キルヒホッフ-ヘルムホルツの積分定理は5図に示すように,境界面を平面S1と部分球面S2とに分割した後,S2の半径を無限大にすることによって,第1種レイリー積分と第2種レイリー積分に変形される2)。第1種レイリー積分は

で表され,第2種レイリー積分は

で表される。ここで,法線方向nとz軸方向が等しいので,∂nを∂zで置き換えている。第1種レイリー積分または第2種レイリー積分とキルヒホッフ-ヘルムホルツ積分定理とは被積分項が音圧勾配∂p(r, ω)/∂zまたは音圧p(r, ω)だけの項となっている点と,受音領域を囲む閉曲面で積分する代わりに音源と受音領域の間に位置した平面S1だけで積分する点が異なっている。6図にレイリー積分を用いた波面合成の例を示す。
第1種レイリー積分は平面上に配置した両指向性マイクロホンによって音圧勾配∂p(r, ω)/∂zを観測し,この信号を用いてモノポール音源を駆動することで原音場を再現する。一方,第2種レイリー積分は平面上に配置した全指向性マイクロホンによって音圧を観測し,この信号を用いて-z方向に主軸を持つダイポール音源を駆動して,原音場を再現する。レイリー積分に基づく音場再現も原空間で観測された信号を別空間で再現してその音場を再現するということにおいて,2章で述べたキルヒホッフ-ヘルムホルツの積分定理を用いた方法と同じである。
これに対して,Berkhoutらはレイリー積分に基づいて音場を合成するWFSを提案した5)6)。WFSは原空間における収音系と再生空間における再生系を分離して扱うことが特徴である。なお,WFSでは無限平面上に2次元的にスピーカーを並べる代わりに1次元的にラインアレイスピーカーを並べて近似再生を行う方法が一般的である。7図にWFSにおける収音・再生系を示す。WFSでは原空間の代わりに仮想的な空間を想定し,仮想空間での音の伝搬を模擬した信号を再生系に入力する。例えば,仮想空間において22.2マルチチャンネル音響7) の前方11チャンネルのスピーカー位置に音源を設置し,それによって得られる波面をアレイスピーカーで合成することで,22.2マルチチャンネル音響コンテンツの前方の音をWFSで再生することが可能となる。
WFSの研究開発はヨーロッパにおいて盛んであり,平板パネルの後ろに数個のアクチュエーターを付けたMulti-actuator PanelによるWFSシステムをフランスのIRCAM(国立音楽音響研究所)が開発している。また,ベルリン工科大学ドイツテレコム研究所の円状スピーカーアレイを用いたWFSサークル,ドイツのフラウンホーファーIDMT(Institute for Digital Media Technology)研究所のWFSシアターなどがよく知られている8)。更に,最近では,車載用のWFSシステムも開発されている9)。



4. 球面調和関数展開に基づく音場再現
Cooperと志賀は受音点で観測される音の方向をフーリエ表現する手法を提案している10)。ある受音点に入射する音の方向パターンを角度θの関数S(θ)で表すと,S(θ)は8図のように,方向に依存しない定数成分と1次のcos成分,sin成分,2次のcos成分,sin成分…という形に分解できる。定数成分に対応する指向性を持つ収音デバイスは全指向性マイクロホンであり,1次の成分に対応する収音デバイスは両指向性マイクロホンである。従って,全指向性マイクロホンを利用して定数成分が,両指向性マイクロホンを利用して1次の係数が観測できる。このような音の方向パターンに基づいて,Gerzonはモノフォニックから2チャンネルステレオ,水平面内のサラウンド,3次元音響までを階層的に記述するアンビソニックス方式を提案した11)。アンビソニックスでは,受音点における音圧を後に示す球面調和関数で展開し,一定次数以上の展開係数を無視することで音の方向パターンを近似的に表す。9図に0次と1次だけを利用した場合のアンビソニックス空間収音方式を示す。9図においてWは全指向性マイクロホンの指向特性であり,これを用いて0次の展開係数を観測する。X,Y,Zはそれぞれx軸,y軸,z軸方向に主軸を持つ両指向性マイクロホンの指向特性であり,1次の展開係数を観測する。また,近年ではアンビソニックスの考え方を拡張し,高次の展開係数まで用いて,音の到来方向を球面調和関数展開する方法の研究が盛んである*3。以下,拡張されたアンビソニックスについて解説する13)。
任意の方向(Ψ, Φ)から平面音波が到来する場合を考える。ここに,Ψは到来方向の方位角,Φは到来方向の仰角である。また,10図に示すようにベクトルrで表される受音点Pの方向を(θ, φ)とし,原点からの距離をrと表す。点Pは直交座標で

と表される。ここで,Tは転置行列を表す。このとき,受音点Pでの音圧は球面調和関数を用いて,

と展開できる4)。ここに,Qは音源の出力であり, はYの複素共役である。また,jn(z)は第1種球ベッセル(Bessel)関数*4 であり,動径方向(r方向)の音圧の変動を表す。また,
はYの複素共役である。また,jn(z)は第1種球ベッセル(Bessel)関数*4 であり,動径方向(r方向)の音圧の変動を表す。また,

は球面調和関数15)*5 であり,角度方向での音圧の変動を表す。球面調和関数における は第1種ルジャンドル(Legendre)陪関数*6 であり,
は第1種ルジャンドル(Legendre)陪関数*6 であり,

で表される15)。ただし,(9)式の{ }内はxのベキ乗の係数が0になる項で打ち切られる。
いま,原点を中心とした半径σの球面上にN個配置されたスピーカーによって,方向(Ψ, Φ)から到来した平面音波の受音点Pにおける音圧を合成する問題を考える。この際,受音点は球の内部に含まれる(r<σ)とする。11図にこの様子を示す。いま,l番目のスピーカー方向を(θl, φl),そのスピーカー入力をal(k)とし,スピーカーからの音波も平面波で近似すると*7,N個のスピーカーによる合成音圧は(7)式と同様に球面調和関数展開により

で表される。(7)式と(10)式が一致した場合に,(Ψ, Φ)方向から到来した音波がスピーカーによって再現される。この条件を球面調和関数の直交性を用いて解き,展開次数nを一定数Mまでに制限することでアンビソニックスの基本式

が得られる。(11)式の右辺は(Ψ, Φ)方向から到来した音波の直交展開係数を表し,左辺はN個のスピーカーで再生した音波の直交展開係数を表す。
以下,(11)式で展開次数を1までに制限した場合(M=1)について計算した例を示す。第1種ルジャンドル陪関数は

なので,1次のアンビソニックスの場合の基本式は

となる。(13)式の第2式と第4式の和および差から,

が得られる。(13)式と(14)式より

を得る。(15)式の右辺はそれぞれ9図のW,X,Y,Zマイクロホンによって観測される信号である。また,(15)式の左辺の角度θl, φl(l=1, …, N)はスピーカー位置で規定されている。従って,(15)式を満たす信号al(k)をスピーカーに入力することによって到来する音波を再現することができる。
アンビソニックスの収音については,球状のマイクロホンアレイがよく研究されている16)。実際に,32個の小型マイクロホンカプセルを持ち,4次までのアンビソニックス係数を観測できるマイクロホンアレイが商品化されている17)。また,近年の音場再生理論では,球面調和関数展開を用いて音場を表現する手法が主流であ18)19)。更に,3章で述べたWFSとアンビソニックスを統一的に扱う試みもなされている20)。




5. 異なるチャンネル数を持つマルチチャンネル音響信号間の変換
22.2マルチチャンネル音響を家庭で楽しむためには24個のスピーカーを設置する必要があるが,24個のスピーカーを設置することが困難な場合がある。そこで,チャンネル数やスピーカー配置が異なるシステムにおいて,それぞれのシステムで再生した音の物理量を受音点で同じにするための信号変換の研究を進めている21)。この方法は2章や3章で述べたような,原音場の波面を再現する方法ではなく,ミキシングスタジオなどで作られた音場(原空間の音場)を別空間で再現する方法である。提案する方法では4章で述べた方法と同様に,受音点での音の方向を再現する。12図に信号変換方式のブロック図を示す。
まず,スピーカーからの音波を(2)式のモノポール関数で表す。従って,原空間でのスピーカー数がnの場合には,原空間の音場はn個のモノポール関数の和で表される。音波の方向を考慮すると,原空間での音響物理量は3次元のベクトル量で表される。従って,12図に示した原空間での音響伝搬特性*8 Hdはスピーカー信号を3次元の音響物理ベクトルに変換する3×n行列となる。同様に,再生空間での音響伝搬特 は3×m行列となる。求める変換行列Wは方程式
は3×m行列となる。求める変換行列Wは方程式

を満たすが,実際には(16)式はx,y,z成分による3つの式の連立方程式なので,m>3の場合には,式の数よりも変数の数が多い劣決定問題*9 となり,解の数は無数に存在する。そこで,無限個ある解の中から解析的な解*10 を得るために,再生空間を隣り合う3つのスピーカーを頂点とする三角形で分割する。すなわち,提案する方式は再生空間の隣り合う3つのスピーカーを利用して原空間のスピーカー位置に仮想音像を形成する方式となる。
提案する方式を用いて,22.2マルチチャンネル音響の低音効果用のLFE(Low Frequency Effect)チャンネルを除いた22チャンネル信号をさまざまなスピーカー配置に対応した少ないチャンネル数の信号に変換して,その再生音の空間的印象を評価した。音の空間的印象としては音の方向と音による包み込まれ感を用いた。評価法には隠れ基準付き3刺激2重盲検法22) を用いた。この方法は22チャンネルの音を基準音として,2つの評価音を1表に示す5段階評価で評価するものである。2つの評価音の1つは基準音と同じであり,これを隠れ基準と呼ぶ。もう1つの評価音はチャンネル数を減らした音である。チャンネル数を減らした音に対する評価値から,隠れ基準音に対する評価値を差し引いた差分値(Difference Grade)で評価する。まず,上層/中層/下層のスピーカー数が9/10/3である22チャンネル信号から3種類のスピーカー配置に対応する10チャンネル信号に変換した場合について実験を行った。3種類のスピーカー配置の上層/中層/下層のスピーカー数はそれぞれ4/5/1,3/6/1,3/5/2である。38人の被験者に対して主観評価実験を行った結果,2種類の空間的印象に対する差分値はいずれのスピーカー配置に対しても-0.8以上であった。そこで,更にチャンネル数の少ない8チャンネル,6チャンネルの信号に変換して実験を行った。各チャンネル数に対して,3種類ずつのスピーカー配置を用意した。8チャンネルスピーカー配置の上層/中層/下層のスピーカー数は3/4/1,2/5/1,2/4/2であり,6チャンネルの場合は2/4/0,1/5/0,1/4/1であった。32人の被験者に対して主観評価実験を行った結果,8チャンネルに変換した場合には2種類の空間的印象に対する差分値は-1.0程度であるが,6チャンネルに変換した場合の差分値は-1.0以下となることがわかった。すなわち,22チャンネルを8チャンネルまで減らした場合においては,音の印象の変化が気にならないレベル(差分値-1.0以上)に保つことができることがわかった。

| 5.0 | 違いがわからない |
|---|---|
| 4.0 | 違いがわかるが気にならない |
| 3.0 | 違いがやや気になる |
| 2.0 | 違いが気になる |
| 1.0 | 違いが非常に気になる |
6. おわりに
音場の波面を正確に再現することを目指した音場再現方式について,現在の研究動向およびその背景となる理論を紹介した。2チャンネル音響やマルチチャンネル音響は音場の波面の正確な再現を目指した方式ではなく,スタジオなどで臨場感の高い音場を作るためのシステムである。しかし,マルチチャンネル音響間の信号変換を行う際には,5章で述べたように音圧などの音響物理量の一致という手法に頼らざるを得ない。一方,音響物理量の再現を目指したWFSでは,それを普及させるために,再生音の劣化がわからない範囲でスピーカー数を削減する試みが行われている。今後の高臨場感音響システムは音響物理量の可能なかぎりの正確な再現と,人間に知覚されない範囲内での近似的な再現とのバランスを考慮して発展していくと思われる。